Activité - Approcher une aire
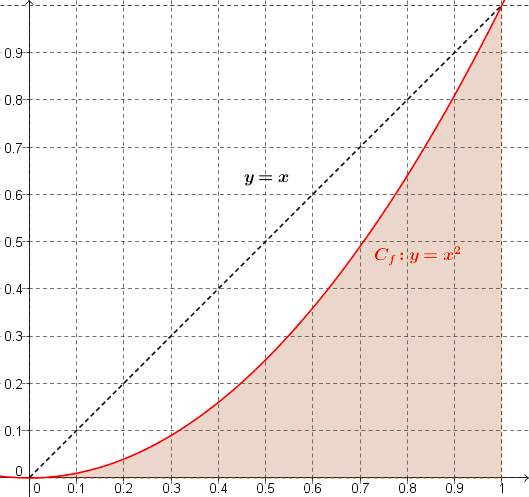
Danc cet exercice, on cherche à évaluer l'aire \(\int_0^1{t^2 dt}\) de la zone coloriée sous la parabole entre 0 et 1, que l'on note \(\mathcal{D}\) :
A1
Tracer sur la figure la droite d'équation \(y=x\). Calculer \(\int_0^1{t dt}\).
2
Tracer sur la figure la droite d'équation \(y=x-0,3\). Calculer \(\int_0^1{t - 0,3 dt}\).
3
En déduire l'encadrement \(0,245 \lt \int_0^1{t^2 dt} \lt 0,5\)
B1
Quelle est l'aire d'un carreau de 0,1 unités de large ?
2
Délimiter la plus petite zone possible, ne comprenant que des carreaux entiers, qui contienne la zone coloriée
. 3
En déduire une majoration de l'aire coloriée
4
Délimiter la plus grande zone possible, ne comprenant que des carreaux entiers, qui soit contenue dans la zone coloriée
. 5
En déduire une minoration de l'aire coloriée
6
Donner un encadrement de \(\int_0^1{t^2 dt}\). Quelle est la marge d'erreur ?
CEn s'inspirant des deux parties précédentes, proposer une méthode s'inspirant des deux précédentes pour approcher l'aire coloriée :
-
comme à la partie A, on veut découper des zones obliques
-
comme dans la partie B, on veut découper en plusieurs petites zones
-
on veut être plus précis que dans les deux cas
1
Expliciter la méthode, et tracer les deux zones sur la figure co-dessous : celle contenant \(\mathcal{D}\), et celle contenue dans \(\mathcal{D}\).
2
Calculer les aires de ces deux zones
3
Proposer un encadrement de l'aire de \(\int_0^1{t^2 dt}\).
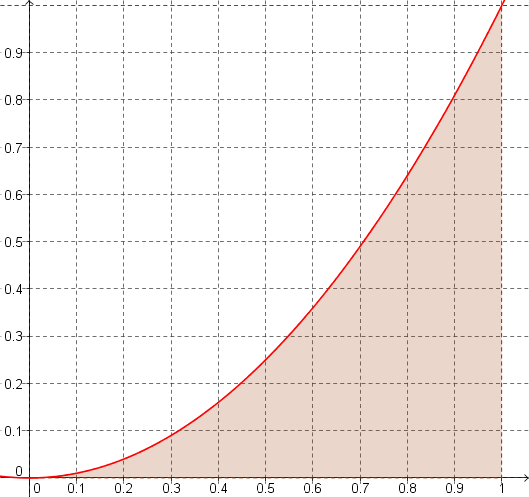
- comme à la partie A, on veut découper des zones obliques
- comme dans la partie B, on veut découper en plusieurs petites zones
- on veut être plus précis que dans les deux cas
D1
Tracer la courbe dans votre calculatrice pour \(x\) dans \([0;1]\) et \(y\) dans \([0;1]\).
2
À l'aide de la calculatrice, donner une valeur approchée à 0,001 de \(\int_0^1{t^2 dt}\)
Pour calculer une intégrale sur la calculatrice, il faut commencer par tracer la courbe, puis :
-
Dans la TI82, aller dans calculs (2nde + trace), puis sélectionner \(\int{dx}\). Avec les touches ← et →, sélectionner les bornes (0 et 1).
-
Dans la Casio, aller dans G-Solve (F5), puis sélectionner \(\int{dx}\). Avec les touches ← et →, sélectionner les bornes (0 et 1).
- Dans la TI82, aller dans calculs (2nde + trace), puis sélectionner \(\int{dx}\). Avec les touches ← et →, sélectionner les bornes (0 et 1).
- Dans la Casio, aller dans G-Solve (F5), puis sélectionner \(\int{dx}\). Avec les touches ← et →, sélectionner les bornes (0 et 1).